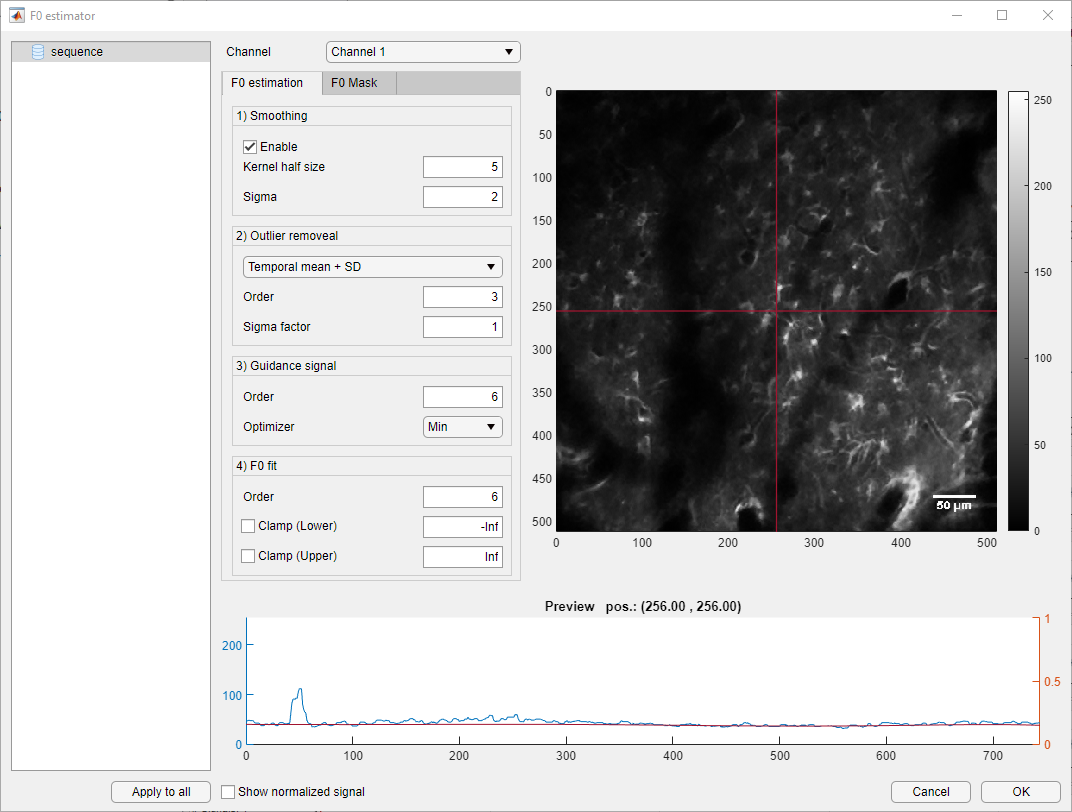
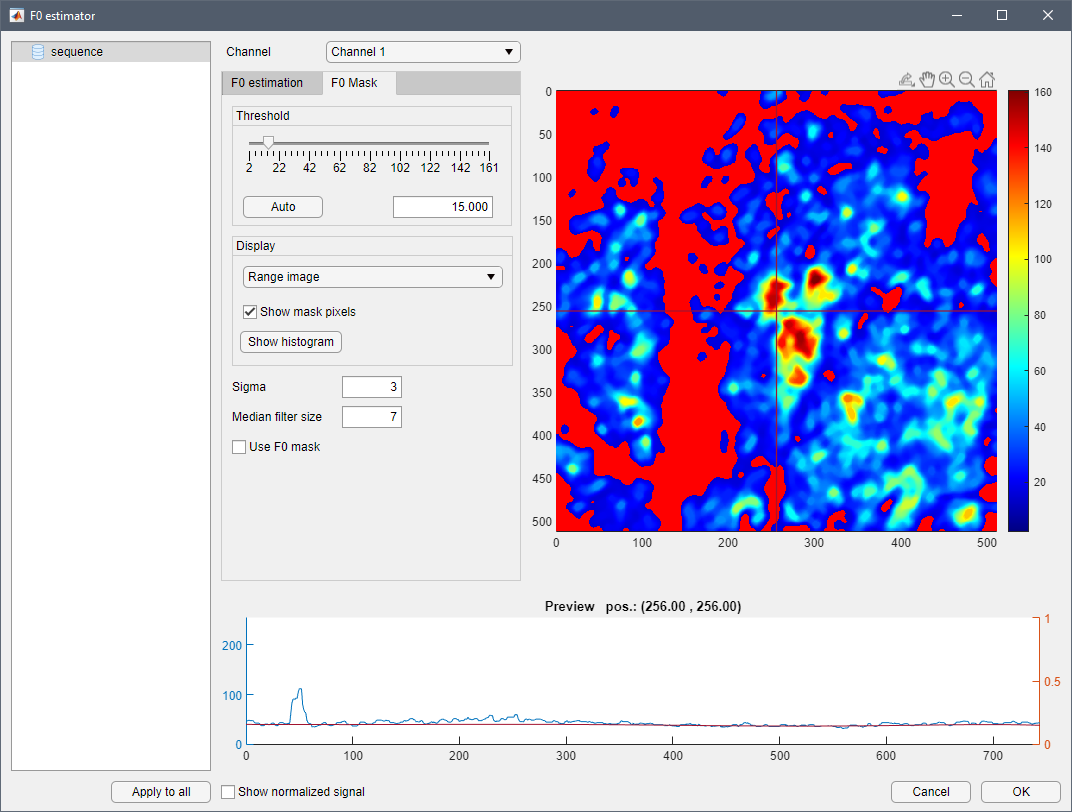
140x140F0 estimation

In MSparkles the analysis of fluorescent signals is based on the background subtracted and normalized signal ΔF/F0 = (F - F0)/F0, where F0 is the basal background and F is the fluorescent signal. When working with ratiometric data, this is a straight forward operation, since typically both channels are contained in the dataset. When processing non-ratiometric data however (e.g. when GCaMPs are used as fluorescence indicator), F0 is typically not readily available. To solve this problem, MSparkles comes with an algorithm to estimate the basal background F0. 

140x140

The F0 estimator dialog allows you to optimize the calculation of the basal background for various scenarios. For example, you can choose to optimize the F0 calculation to adapt to local or global trends, using a Hampel filter or a temporal mean filter, respectively. This way you can precisely configure to which phenomena the background estimator should adapt to.
F0 estimation is performed along the temporal axis for each individual pixel by fitting a polynomial curve. In order to fit the polynimoal to the background signal and not the actual fluorescence signal, some cleanup steps are required beforehand. The first step hereby is to remove peaks, either by using a Hampel filter or a temporal mean filter. The Hampel filter uses a sliding window approach and is thus suited to follow local brightness changes. The temporal mean filter on the other hand operates on a pixels entire temporal course and tries to find a globally minimial baseline. Next, the cleaned-up signal is approximated by a piecewise constant function. This helps to eliminate oscillations at the start and the end of the signal in the subsequent least-squares polynomial fit.


F0 masking is a powerful tool to effectively explude pixels from further analysis. For example, a field of view may contain areas with little (e.g. just noise) or no fluorescent activity at all. Silencing these pixels has an beneficial impact on performance, since fewer computations need to be done. But, besids accelerating computations, F0 masking can also have a positive effect by reducing the chance of false positive detection. Consider, for example, an almost black pixel with no fluorescest activity, where only some (detector) noise is present. This pixel typically has values close to 0, which results in F0 being also close to 0 or 0 in some places. This will very likely cause very high peaks or even values going to ∞ during the ΔF/F0 calculation, which will in turn cause the ROI-detector to create false-positives, or artificially enlarge real ROIs.
F0 masking is based on the fluorescent range map of the dataset. This allows to effectively identify pixels with no or only weak fluorescent activity within the dataset. Pixels excluded by F0 masking will not undergo the baseline estimation, but be assigned the exact values from the (pre-processed) dataset, F. This wffectively sets them to 0 during the ΔF/F0 computation and thus renders these pixels "invisible" for the ROI detector.

140x140